I have a CNC mill and a desire to make circuit boards. Naturally, I need to create tool paths for these circuit boards and cut them out with my mill.
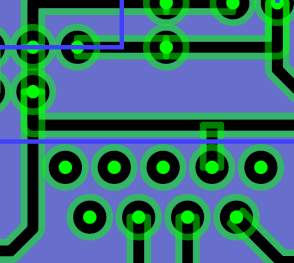
I have created a JavaScript application to create SVG images of the circuit traces and landings, but now I need to determine the path around all traces and landings that intersect each other. Since all of my traces are poly lines, and my landings are either circles or rectangles, it’s super easy to just add width to the SVG objects and get paths around each trace or landing individually. Now I need to string together intersecting paths and cut out the parts I don’t want. This will require knowing the intersection points of lines with line, lines with arcs, and probably arcs with arcs. Let’s get started.
Line to Line
Our saga begins with the parameterization of a humble line, $\vec{p}=\vec{m}t+\vec{b}$. This expression differs from the usual algebra I form by using vectors for the slope and intercept. I do this to avoid infinite slope, when the line is vertical, and to take advantage of a little extra flexibility. When determining the slope and intercept of a line we simply say that the equation hits two points.
$$\left\{\begin{array}{lcc} \vec{m}t_0+\vec{b} & = & \vec{p_0} \\ \vec{m}t_1+\vec{b} & = & \vec{p_1} \end{array}\right.$$
Here the points are $\vec{p_0}$ and $\vec{p_1}$. We would then just solve for $\vec{m}$ and $\vec{b}$. The thing is, there’s nothing about the problem that requires us to choose anything in particular for $t_0$ and $t_1$, except that they can’t be the same. This gives that extra flexibility.
I’ll set $t_0=0$ and $t_1=1$. That way, the equations are easy to solve, and we know that setting $t$ to anything between zero and one will give you a point on the line.
$$\left\{\begin{array}{rcc} \vec{b} & = & \vec{p_0} \\ \vec{m}+\vec{b} & = & \vec{p_1} \end{array}\right.\rightarrow \left\{\begin{array}{ccl} \vec{m} & = & \vec{p_1}-\vec{p_0} \\ \vec{b} & = & \vec{p_0} \end{array}\right.$$
Now let’s use this general line to describe a line segment from $\vec{p_0}$ to $\vec{p_1}$ and another from $\vec{v_0}$ to $\vec{v_1}$, then figure out where those two lines describe the same point.
$$(\vec{p_1}-\vec{p_0})t_p+\vec{p_0}=(\vec{v_1}-\vec{v_0})t_v+\vec{v_0}$$
Through the magic of 2D vectors, this is actually a system of two equations and two unknowns, $t_p$ and $t_v$.
$$\left\{\begin{array}{rcrcl} (p_{1x}-p_{0x})t_p & – & (v_{1x}-v_{0x})t_v & = & v_{0x}-p_{0x} \\ (p_{1y}-p_{0y})t_p & – & (v_{1y}-v_{0y})t_v & = & v_{0y}-p_{0y} \end{array}\right.$$
If we solve for just one of the variables, let’s say $t_p$, and substitute it into its equation, then we’ll know where the lines intersect. Or we’ll know where the lines would intersect if they went on forever. What we really want is to know where the point is, and if it is on both line segments. Here’s the second reason I chose $t_0=0$ and $t_1=1$. If $t_p$ and $t_v$ are both between zero and one ($t_p,t_v\in[0,1]$), then the intersection point is on both segments, and if they’re not both between zero and one, then the point isn’t on both segments. And just like that we have the arithmetic and logic needed for a computer to spit out and intersection point.
- $t_p=\frac{(v_{0x}-p_{0x})(v_{1y}-v_{0y})-(v_{1x}-v_{0x})(v_{0y}-p_{0y})}{(p_{1x}-p_{0x})(v_{1y}-v_{0y})-(v_{1x}-v_{0x})(p_{1y}-p_{0y})}$
- $t_v=\frac{(p_{1x}-p_{0x})(v_{0y}-p_{0y})-(v_{0x}-p_{0x})(p_{1y}-p_{0y})}{(p_{1x}-p_{0x})(v_{1y}-v_{0y})-(v_{1x}-v_{0x})(p_{1y}-p_{0y})}$
- $\vec{p}=(\vec{p_1}-\vec{p_0})t_p+\vec{p_0}$
- $t_p\in[0,1]\land t_v\in[0,1]\Leftrightarrow\text{the line segments intersect}$
Line to Arc
At first glance intersecting an arc with anything seems like it should be more difficult than just a couple of lines. But, while this problem isn’t quite as straightforward, it isn’t pear shaped either.
The easiest way to think of intersecting a line and an arc is to think of the points on a line that are some fixed distance away from the center of a circle. If we define a line like above, then we’re just looking for the value of $t$ where the length of the vector from the arc’s center ($\vec{c}$) to a point on the line is equal to the arc’s radius ($r$).
$$\left|\vec{p_1}-\vec{p_0}t+\vec{p_0}-\vec{c}\right|=r$$
Knowing the sum of squares definition of vector length and a bit of off-screen algebra yields a friendly quadratic to solve.
$$\begin{array}{l} a_2t^2+2a_1t+a0=r^2 \\ \Rightarrow t=\frac{-a_1\pm\sqrt{a_1^2-a_2(a_0-r^2)}}{a_2} \end{array}\ \ni\ \left\{\begin{array}{l}a_2=(\vec{p_1}-\vec{p_0})\cdot(\vec{p_1}-\vec{p_0}) \\ a_1=(\vec{p_1}-\vec{p_0})\cdot(\vec{p_0}-\vec{c}) \\ a_0=(\vec{p_0}-\vec{c})\cdot(\vec{p_0}-\vec{c}) \end{array}\right.$$
If the solutions for $t$ are complex, then the line does not intersect the arc. However, like the line segment problem, if the solutions are real, we can only say that the infinitely long line would hit a circle around point $\vec{c}$. To say the line hits the arc takes a little more work.
To start with, let’s barrow from the line to line problem and say that any solution for $t$ that is not between zero and one is not one the line segment. From here I’m inclined to calculate the angle for the start of the arc, the end of the arc, and the proposed intersection point. To do this we’ll use a little trigonometry and some logic. We can say that the cosine of the angle is the horizontal component of the vector from the center to a point, divided by the length of that vector. All you have to do then is take the inverse cosine, and you have an angle. Except there are two angles between 0 and 360°. Conveniently, one option has a positive vertical component to the vector, and the other has a negative vertical component.
$$\theta=\left\{\begin{array}{ll} \cos^{-1}\left(\frac{p_x-c_x}{r}\right), & p_y-c_y>0 \\ \cos^{-1}\left(\frac{p_x-c_x}{r}\right)+180^\circ, & p_y-c_y\le 0 \end{array}\right.$$
Now, I could just be content with that, and move on to comparing the angles, but I feel like asking a computer to calculate inverse cosines is inefficient somehow, especially since all I care about is putting the start, end, and intersection points in order. The $\cos^{-1}x$ is bijective on $x\in[0, 180]$ and from -1 to 1, that is to say the function has a unique output value for every input value (one-to-one and onto). If all we want is to put a few points in order, then we could use any function that is a bijection on that same range. Hell, we could use a line.
$$\hat{\theta}=\left\{\begin{array}{ll} 180\left(1-\frac{p_x-c_x}{r}\right), & p_y-c_y>0 \\ 180\left(1-\frac{p_x-c_x}{r}\right)+180, & p_y-c_y\le 0 \end{array}\right.$$
But, why stop there? I don’t care about the angle values being from 0 to 360. Why not make it simple and multiply everything by $r$ divided by 180?
$$\hat{\theta}=\left\{\begin{array}{ll} r-p_x+c_x, & p_y-c_y>0 \\ 2r-p_x+c_x, & p_y-c_y\le 0 \end{array}\right.$$
Ah, that’s better. Now we can easily calculate values for the beginning of the arc ($\hat{\theta_0}$), the end of the arc ($\hat{\theta_1}$), and the proposed intersection point ($\hat{\theta_p}$). I was going to share the process of creating simple logic to say if an intersection point is on the arc, but my brains went to mush and oozed out of my ear when I tried to explain the process in a paragraph. That will have to wait for another day.
Arc to Arc
Intersecting arcs is more geometric than intersecting lines, with a linear algebra twist at the end. Effectively, we draw a triangle and align it to the vector between the centers of each arc. After finding the intersection points, we use the same angle estimation technique as in the line to arc section to make sure the points are on the actual arcs.
Let’s start with that triangle. In space, we’re dealing with the two triangles with a common base that runs between the centers of each arc ($\vec{c_1}$ and $\vec{c_2}$), where the two other sides are the radii of the two arcs ($r_1$ and $r_2$), intersecting at some point $\vec{p}$. For simplicity, however, let’s think of the line from $\vec{c_1}$ to $\vec{c_2}$ as horizontal.
With this set up, finding the location of $\vec{p}$ is as simple as finding the height of the triangle, $h$, and the horizontal distance from the $\vec{c_1}$ to the $\vec{p}$, $l$. We’ll do this with a double Pythagoras.
$$\left\{\begin{array}{l} l^2+h^2=r_1^2 \\ \left(|\vec{c_2}-\vec{c_1}|-l\right)^2+h^2=r_2^2 \end{array}\right.$$
Which solves nicely down to:
$$\begin{array}{l} l=\frac{r_1^2-r_2^2+|\vec{c_2}-\vec{c_1}|^2}{2|\vec{c_2}-\vec{c_1}|} \\ h=\pm\sqrt{r_1^2-l^2} \end{array}$$
Now, this triangle is aligned horizontally, but we need it to be aligned to the actual points $\vec{c_1}$ and $\vec{c_2}$. To do this we’ll whip out a quick ortho-normal linear transform. Effectively, we’ll multiply a 2×2 matrix by a vector of $l$ and $h$ that would rotate a horizontal vector to align with $\vec{c_2}-\vec{c_1}$ and a vertical vector to be perpendicular to $\vec{c_2}-\vec{c_1}$.
$$\vec{p}=\frac{1}{|\vec{c_2}-\vec{c_1}}\left[\begin{array}{cc} c_{2x}-c_{1x} & -c_{2y}+c_{1y} \\ c_{2y}-c_{1y} & c_{2x}-c_{1x} \end{array}\right]\left[\begin{array}{c} l \\ h \end{array}\right]$$
As you can see, the first column of the matrix is just the vector $\vec{c_2}-\vec{c_1}$ while the second column is that same vector turned clockwise by 90°. This gives both potential intersection points. Now we have only to determine if they are actually on the arcs we started with.
The first hurdle to an intersection point being on an arc is for the two circles, on which the arcs are based, to actually touch. This comes clear when calculating the location of $\vec{p}$. If $l>r_1$ then the circles don’t touch, and $h$ will be imaginary. With that cleared, we can ask if the intersection points are on the arcs. For this we’ll estimate the angles of each start point, end point, and proposed intersection point using the method described in the line to arc intersection section.
$$\hat{\theta}=\left\{\begin{array}{ll} r-p_x+c_x, & p_y-c_y>0 \\ 2r-p_x+c_x, & p_y-c_y\le 0 \end{array}\right.$$
With these angles and knowledge about which direction each arc travels from start to finish (clockwise or counter-clockwise), we can then decide if an intersection point is on both arcs.
Conclusions
This has all been great fun. These three intersection cases give opportunity to play with parameterized functions, linear algebra, geometry, and a hack-and-slash form of trigonometry. Unfortunately, the next step on this quest to create tool paths would require that I write a program to take a bunch of closed paths and splices together all of the paths that intersect, while deleting all segments of those paths that are completely inside other paths. The task isn’t super difficult, but it turns out Eagle CAD has a free hobbyist version and there’s an add-on that generates tool paths from Eagle CAD files. I’m going to use that.